Task 7 requires you to
- Recover TerrorTime user’s private keys
- Decrypt messages
- Determine Terrorist’s action and target
Analyzing RSA Key Generator
I used IDA free to dissemble the key generator. When I first open the program, I found lots of strange function names and it didn’t resemble other binaries I have looked at. I used Google to search one of the functions containing the word “clap”. Clap is used for validating command line arguments to Rust programs. This let me know the program was written in Rust and why I did not recognize anything.I checked the binaries the Android app uses to determine if it was written in a language I was more familiar with.
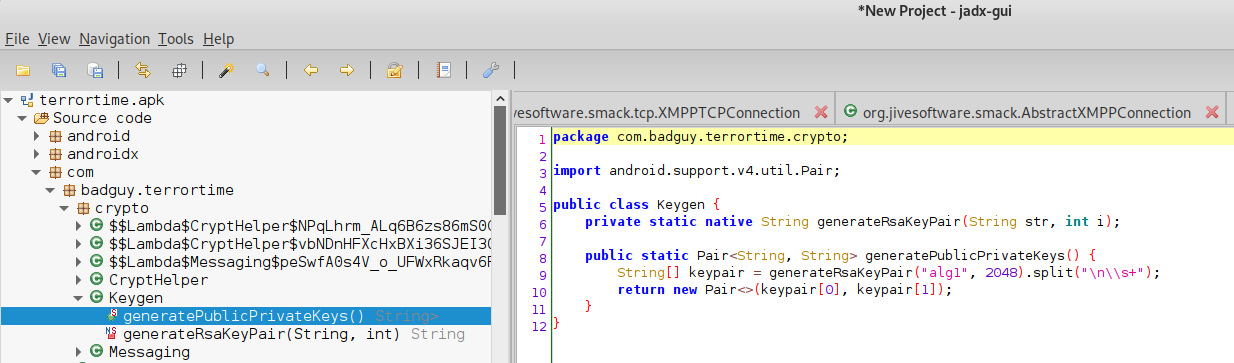
It was also in rust, but I noticed the Android app uses alg1. I found references to two different algorithms in the binary.
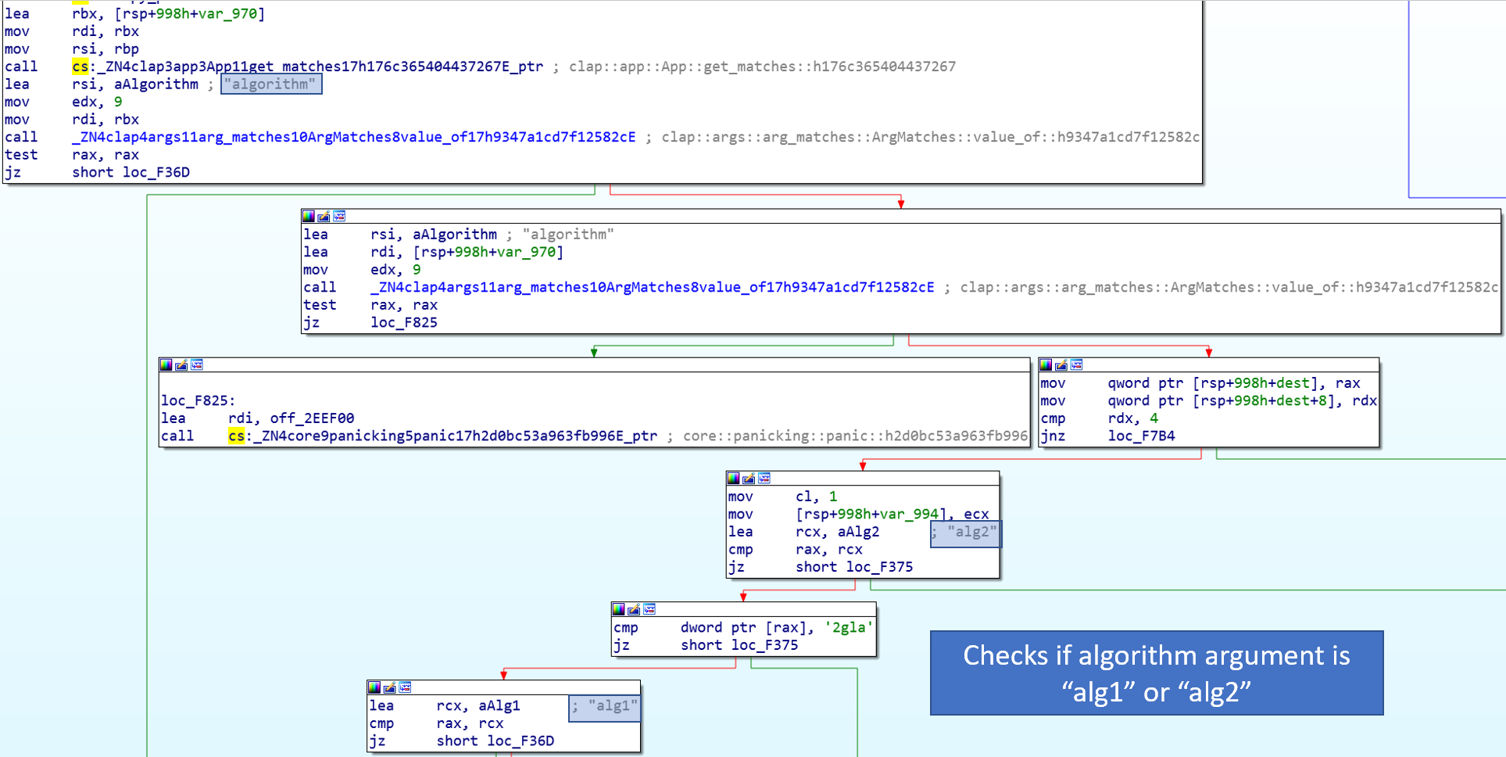
The keygen contains logic to check for the command line argument “algorithm” and choose the algorithm to use based on the value. This argument is not in the help message, and seems to default to alg1. Additionally, there were two functions called RsaAlg1 and RsaAlg2. I decided to compare these functions to determine what was different.
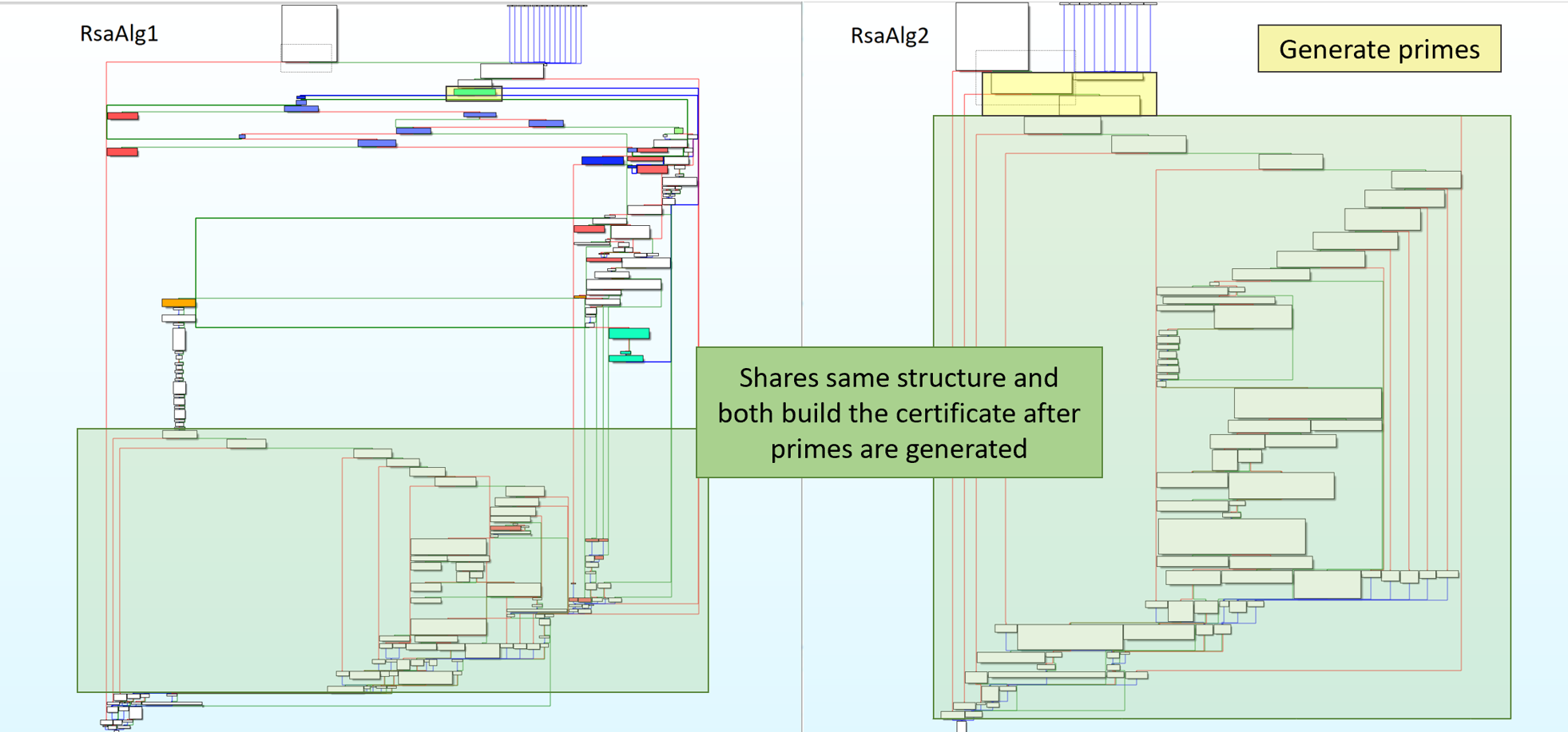
RsaAlg1 has some additional functionality when generating the primes. Additionally, it only generated one prime and the other prime was derived after manipulating the first prime. I decided that this extra code must be where the backdoor is added, since this function is the one used by the app.
I determined a few interesting things when analyzing the Rust binary.
- In Rust, the first argument passed to a function is not a parameter but where the return value is stored.
- Strings are not NULL terminated.
- Returned values had the structure (<error>,<return val>). If the return value is in eax, then [eax] would contain length data and [eax+8] contained the actual value.
- Example, pub fn from_slice(n: &[u8]) -> Result<BigNum, ErrorStack>
- Rust compiles statically, resulting in a large file size.
Research Into Placing Backdoors In RSA
RSA is an asymmetry scheme that is based on the difficultly in factoring extremely large numbers. The public key contains the parameters n and e. The private key contains the parameters n and d. The parameter n is equal to p * q, where p and q are both prime.
Before going further, I did some research on how to backdoor RSA keys to compare methods with what the code was doing. Below are the methods I found.
- Fix primes
- Encrypt prime p and use that as the Public Key parameter e
- Encrypt prime p and place in Public Key parameter n.
- Encrypt prime p and place X number of bits in Public Key parameter n.
Method 2 was introduced by Adam Young and Moti Yung in section three of their paper The Dark Side of Black-Box Cryptography or Should We Trust Capstone. They make the assumption that the public parameter e is normally chosen at random, which is not the case in practice.
Method 3 was also introduced by Adam Young and Moti Yung as Pretty-Awful-Privacy (PAP). They describe PAP as a program that will
- generate prime p,
- use method to scramble p,
- encrypt scrambled p,
- scramble encrypted data,
- set as higher order portion of n,
- randomly generate the rest of n,
- divide n by p to get q,
- check if q is prime.
Method 4 was introduced as RSA-HP by Claude Crepeau and Alain Slakmon in section five of their paper Simple Backdoors for RSA Key Generation to address some of the shortcomings of PAP. The paper mentions hiding only part of the prime p.
More research into RSA backdoors can be found here
Determining Method Used
I determined that the primes were not fixed, since the function makes a call to generate a prime and then derives prime q after performing some work on p.
Method 2 enables the primes to be different than each other, but is easily detectable. Most RSA key pairs set e to be 3 or 65,537. This method will set e to a very large number which makes it detectable when compared to normal RSA key pairs. The keys generated by the keygen program have e set as 65,537.
PAP encrypts the prime p and uses this as a starting point for n. The parameter n is chosen to satisfy prime(n / p) == true, and e is chosen normally. This method is less detectable than method 2, but can still be detected. Normal key pairs have primes with lengths that are powers of two. Since q is not chosen, the length of q can not be set exactly. This results in the length not always being a power of two. Out of 1,000 RSA keys generated with the backdoor, none of them were 2048-bit.

PAP is an interesting method, but has a huge flaw when p is encrypted with RSA. If the prime p is encrypted with RSA key of the same size (half the size of the generated RSA key pair size), then this heavily reduces the security of the resulting RSA key. A better method would be to encrypt prime p with AES since a smaller key size can provide the same level of security, an example is rsabd.py. NIST places 128-bit AES and 3072-bit RSA at the same security level.
Now, I started digging more into the code by looking for interesting functions. I found
- main,
- RsaAlg1,
- RsaAlg2,
- select_key_params,
- permute_r_key, and
- get_r_keys.
The function select_key_params will retrieve 3 embedded strings from the binary based on the requested key size. One string is a public key and the other two strings are base64 encoded r keys.
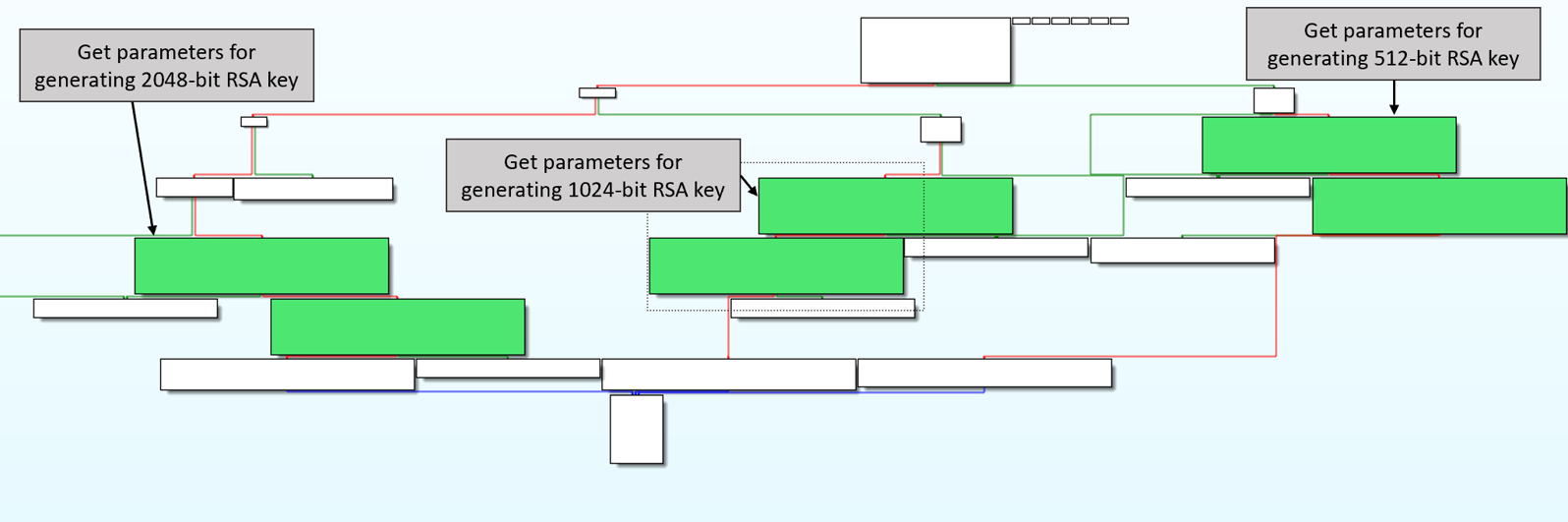
I found the easiest method for understanding RsaAlg1 was to color different blocks and make high level notes on each block’s functionality. I first colored blocks red that were reached due to an error. Next, I colored functions that belonged to the first for loop blue, and highlighted the beginning and end of the second for loop green. Finally, I wrote what each block did based on the functions called. Additionally, I named variables that stored results from different functions. This enabled me to start piecing the code’s functionality together. In the below images, red lines means check failed and green means check succeeded.
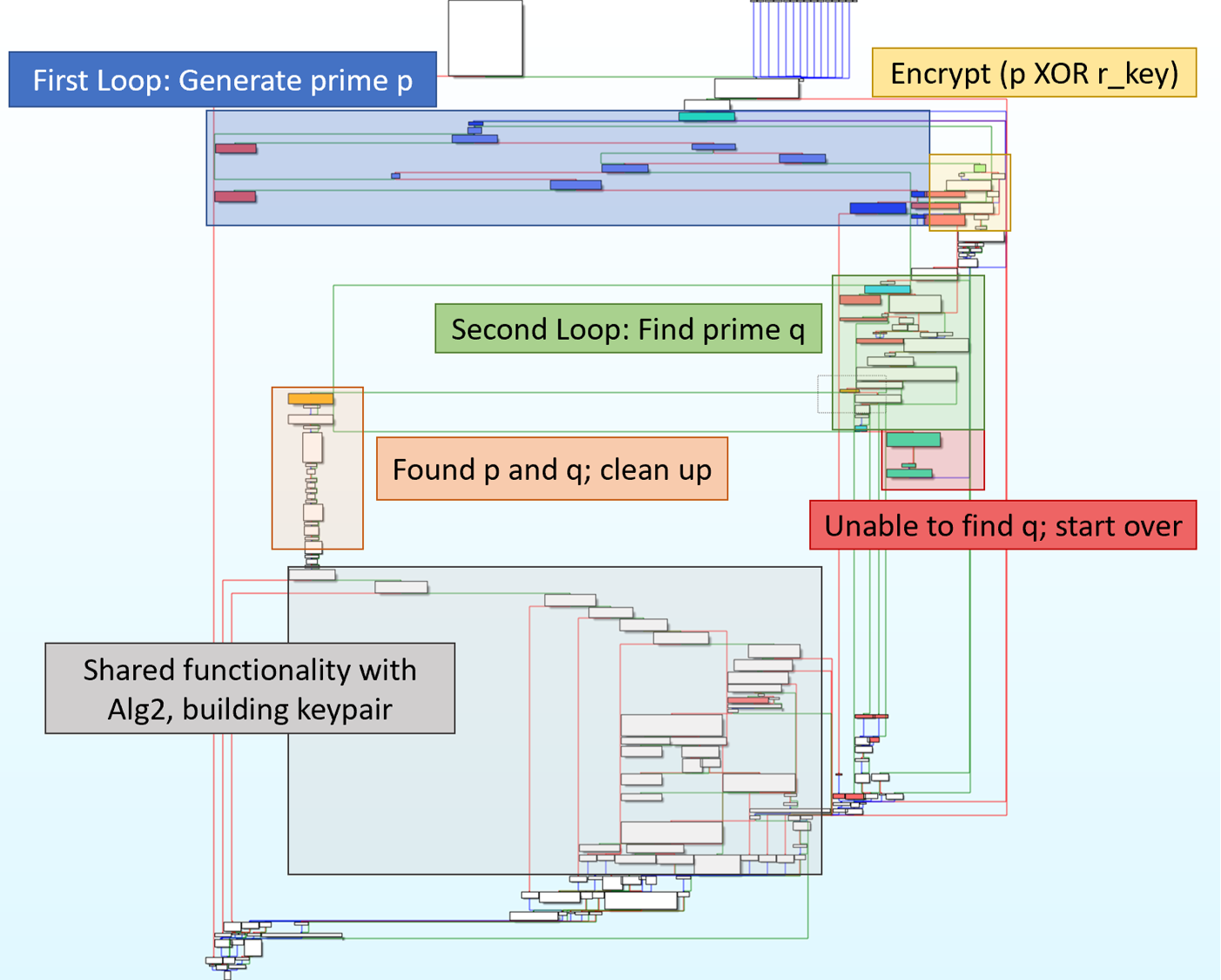
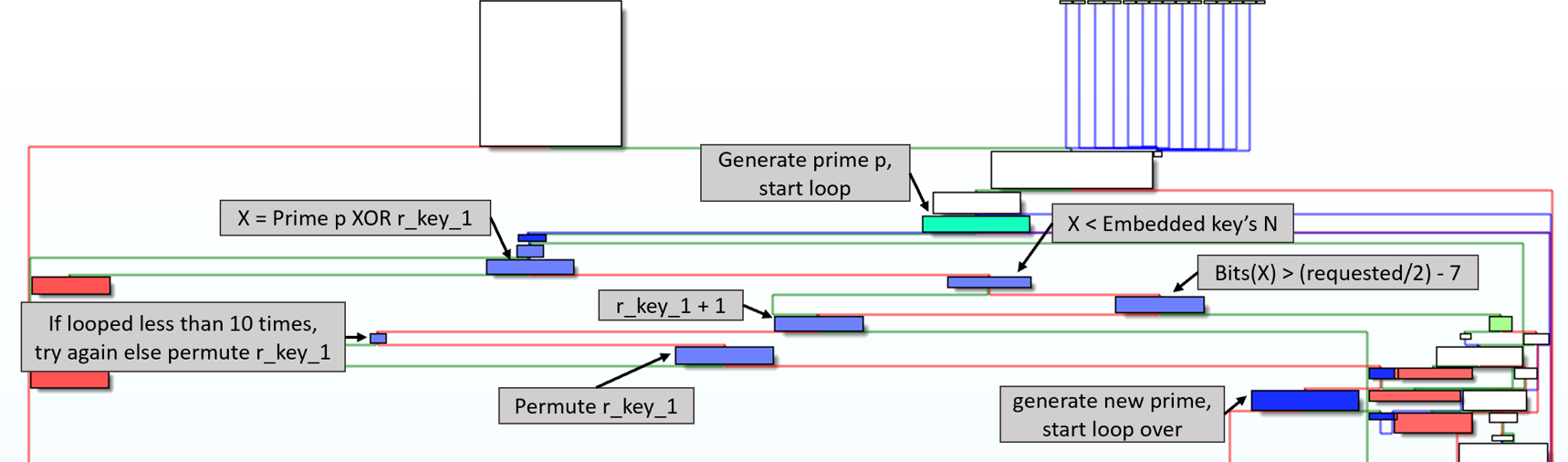
The first for loop will
- generate a prime
- attempt to XOR prime with another value
- check the result
- if it does not pass check, then it will generate another prime
The second for loop will
- encrypt XOR’d prime
- generate random value
- concatenate encrypted prime and random value
- divides result by prime p
- checks if result is prime
- if it is not a prime, then generate a new random value
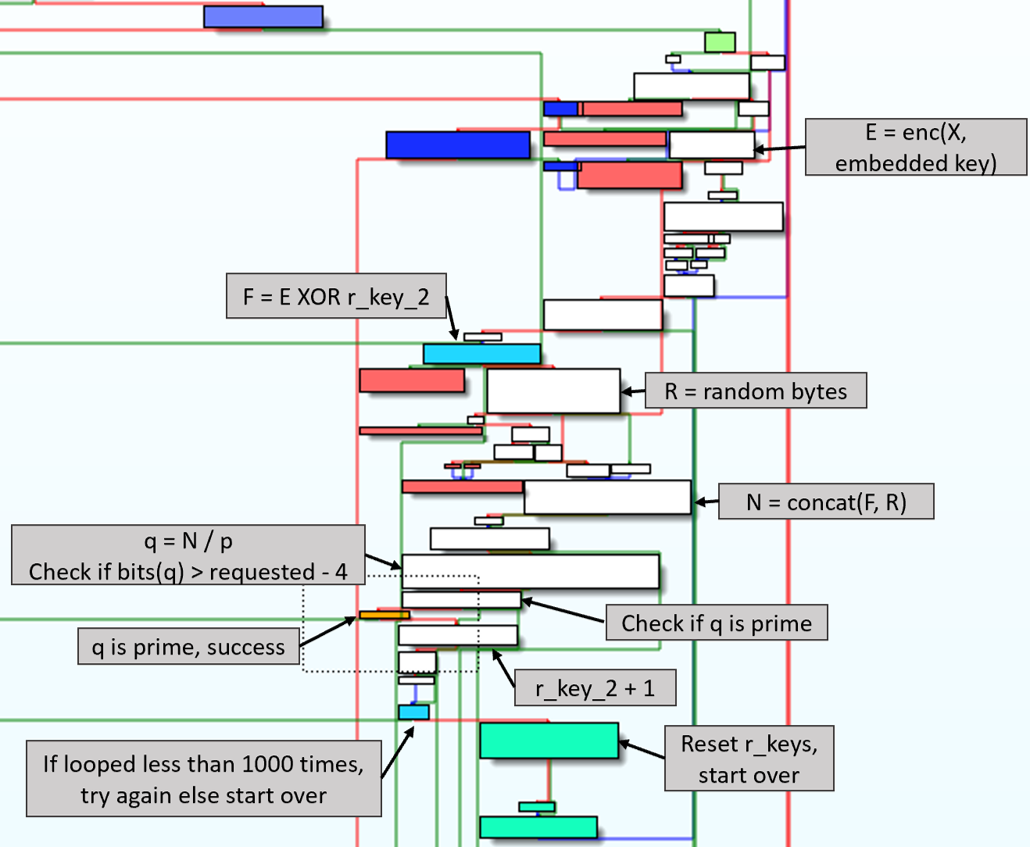
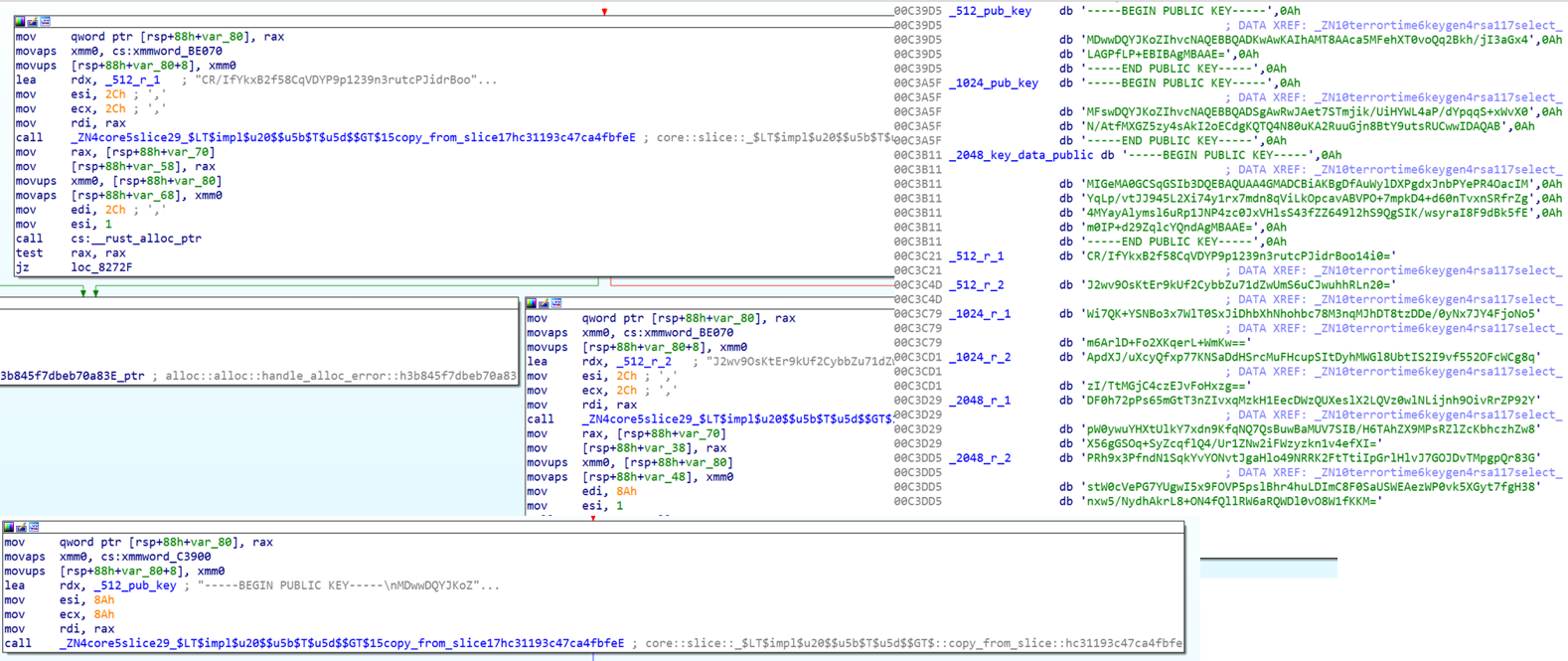
I was able to determine the backdoor scheme they used was a slightly modified PAP by comparing what the code was doing at a high level. It encrypted the prime p and hid it in the public parameter n. PAP was changed to use different values for scrambling prime p before and after encryption. I needed to determine how the XOR values were determined in order to be able to recover prime p from n. Looking at the first XOR, I named the variables to indicate what they were. One was the the result of function generate_safe_prime, the other was unknown.
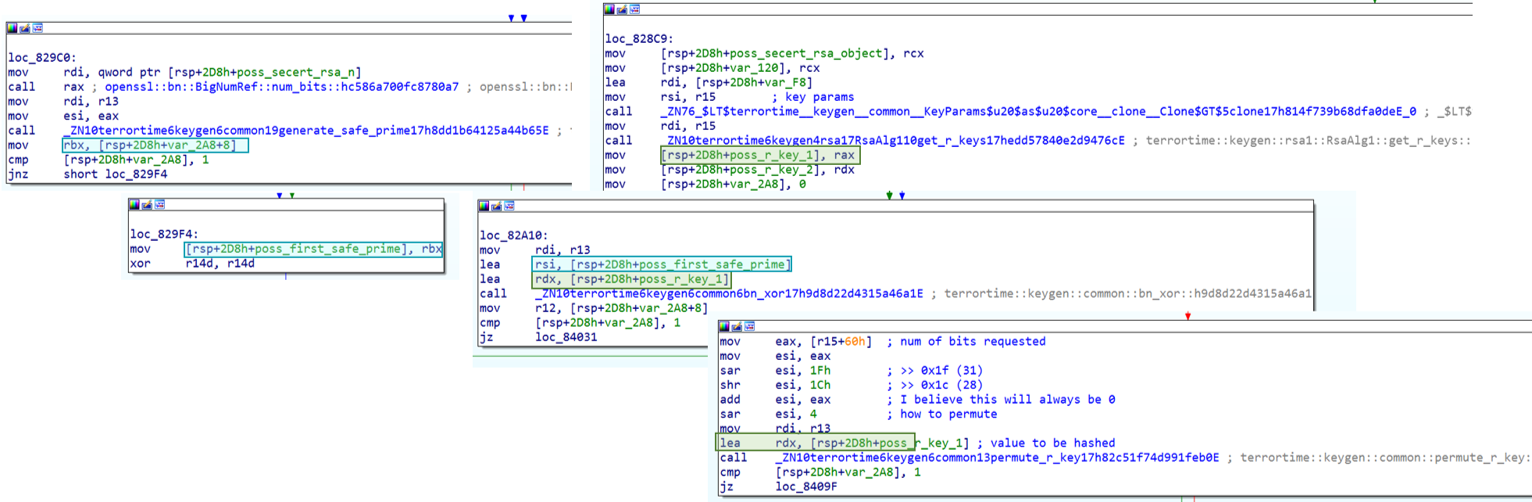
The unknown variable was passed to permute_r_key function and was set with the result from get_r_keys function.
The get_r_keys function base64 decoded two values, which I believed were likely from the select_key_params function. Now, I knew the starting values of the r keys, but needed to investigate the permute_r_key function to determine how they are changed. The function permute_r_key hashes the r key as a method to change it. The hash algorithm is either MD5, SH256 or SHA512 depending on the size of the key requested.
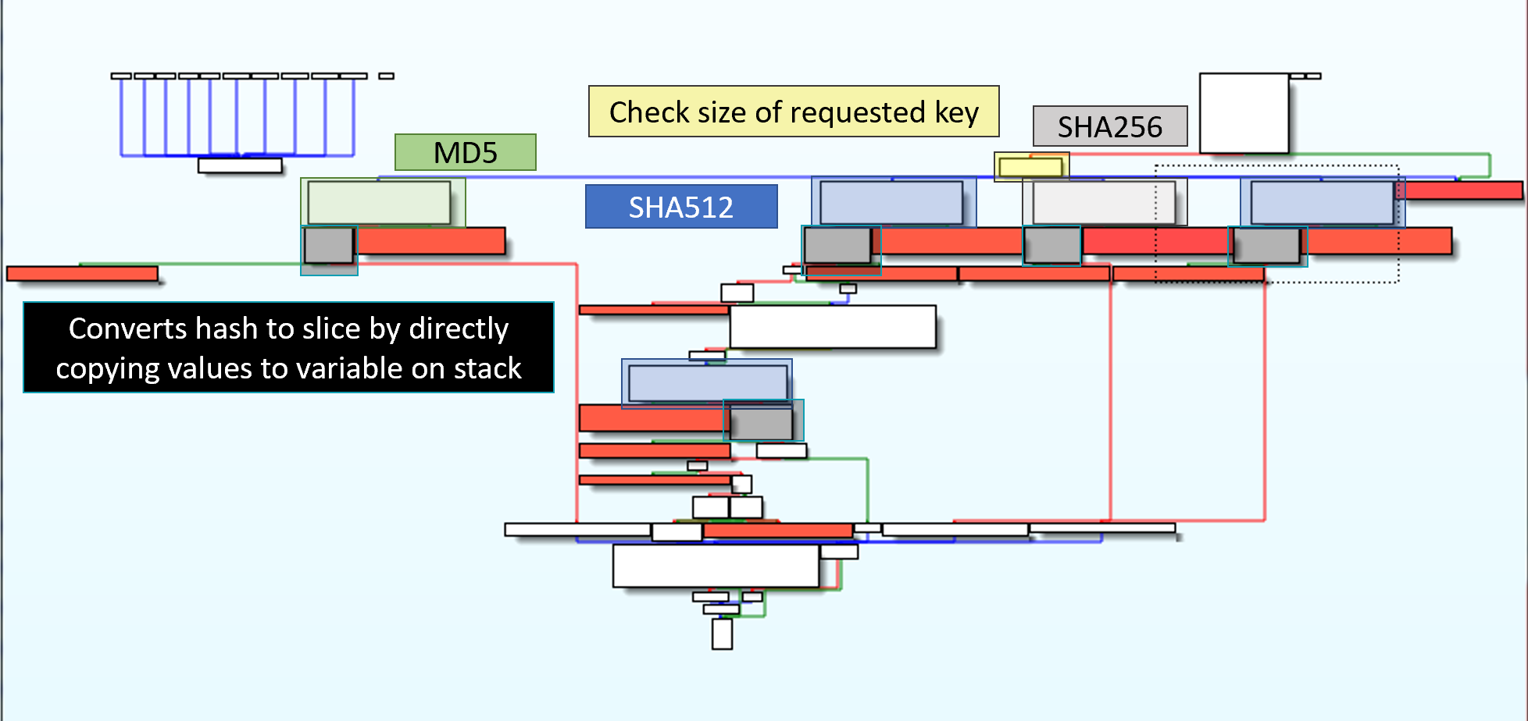
Interestingly, one of the hash algorithms is MD5 which results in a 128-bit result. This might indicate that the programmer had intended for the code to generate 256-bit keys, even though the program only accepts requests for sizes 512, 1024, and 2048. How the resulting hash is converted to a vector is a little confusing. At first, I thought the r key was hashed and the hash was reversed. Instead, The hash value is copied to the stack intact, it only appears that it is being placed in reverse since the stack grow up. I believe this copying is not necessarily required when the hash is SHA256 or a single SHA512. This copying is necessarily for when two SHA512 are used and the results are combined.
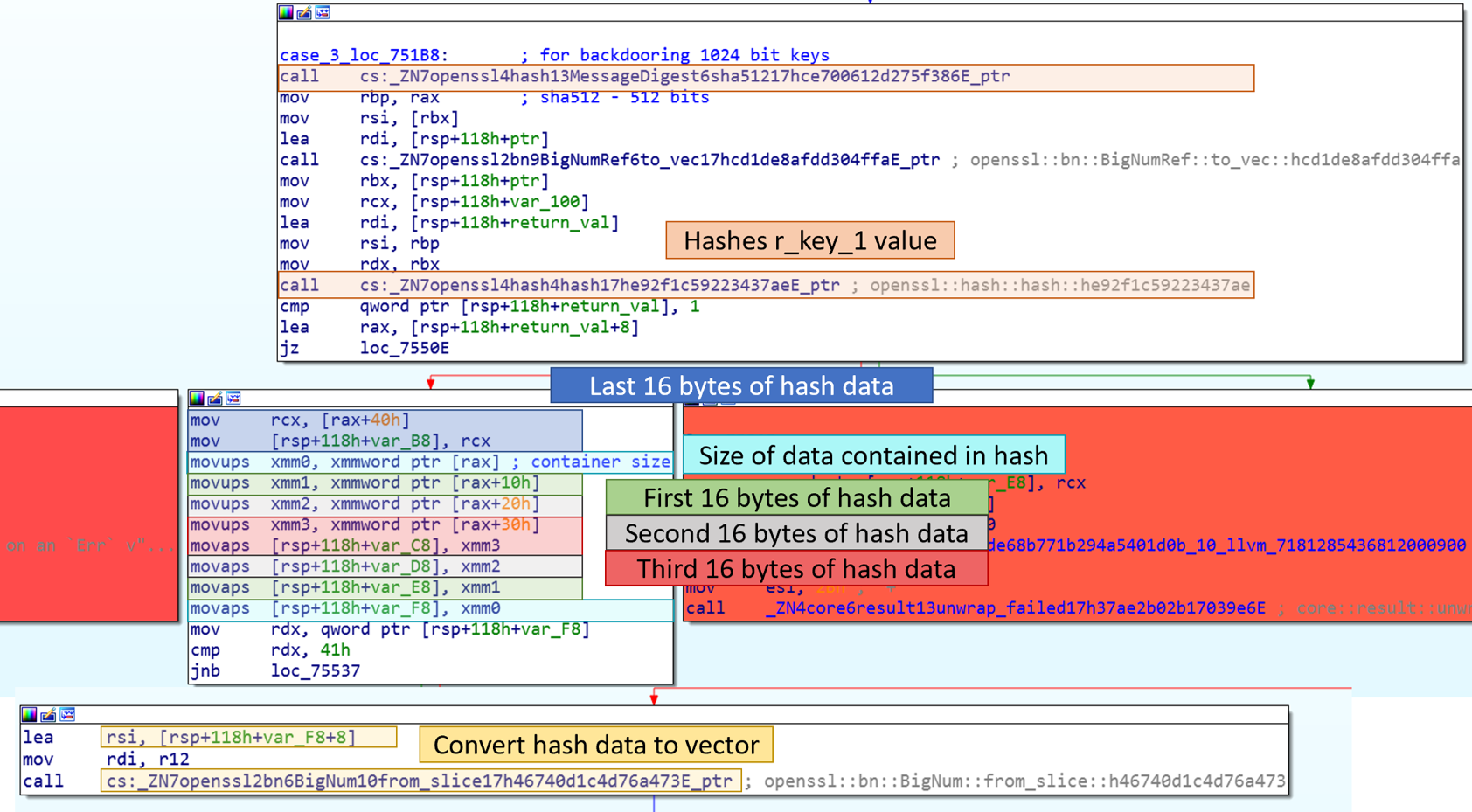
I now was able to put the pieces together to determine how the code backdoored the RSA key. Below is python code that duplicates the process. I used the python code to validate my understanding of the keygen code.

Below is the python code to reverse the process.

I could now extract the prime p from the public value n, except I did not have the private key to decrypt the value p XOR r_key_1. The embedded RSA keys were too big to attempt to factor or attack directly. I thought maybe they used the same RSA key generator as the one to generate the RSA keys for TerrorTime, which would backdoor the RSA key. PAP has an interesting tell, the size of key is very rarely a power of two.
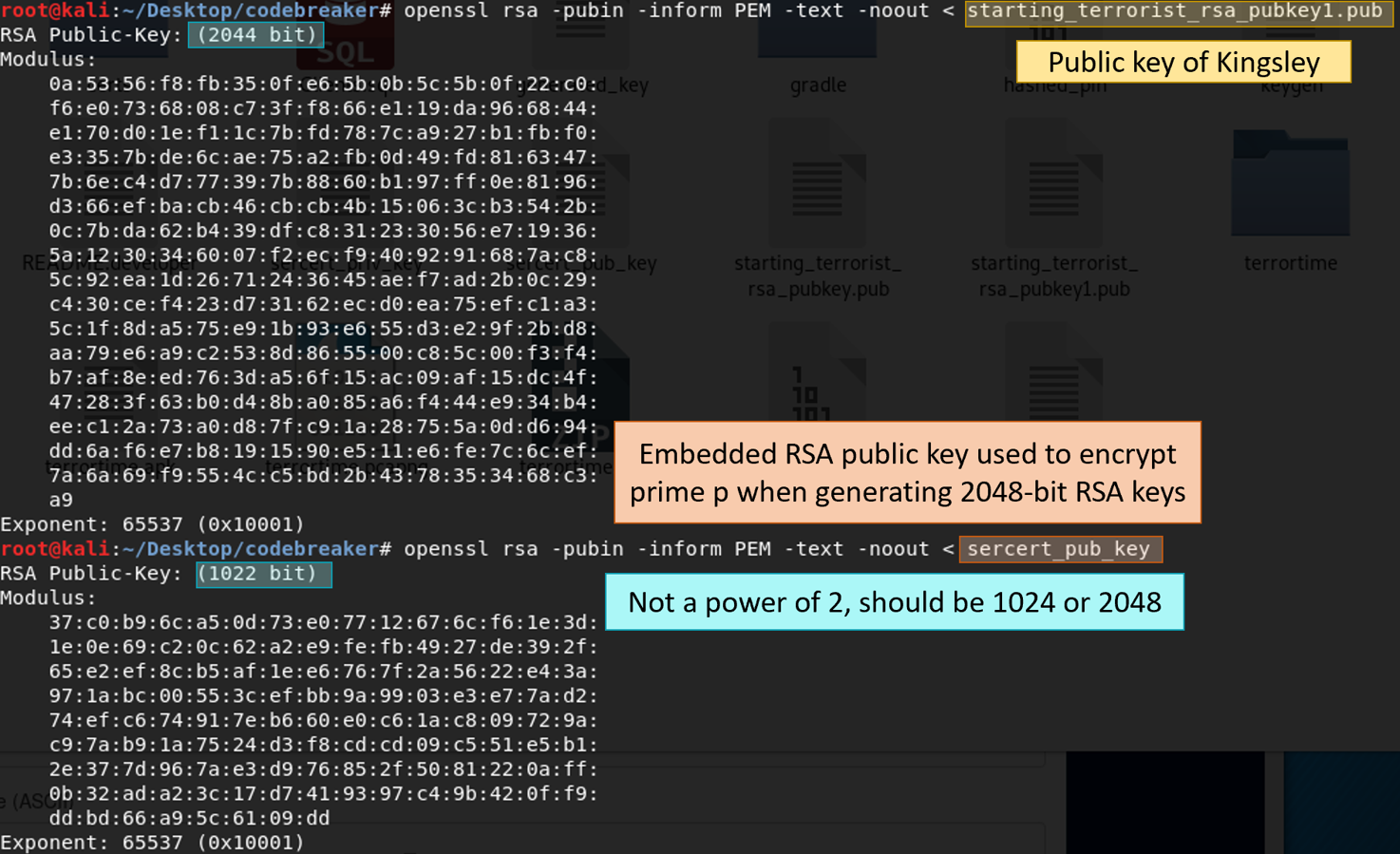
I used openssl to check the key sizes of the embedded RSA keys. It turns out they backdoored their backdoor. This meant I could recover the private key for the embedded RSA key by using the next smaller embedded key. Ex. To recover the private key for the RSA public key used to encrypt the prime for 2048-bit keys, I needed to recover the private key for the RSA public key used to encrypt the prime for 1024-bit keys.
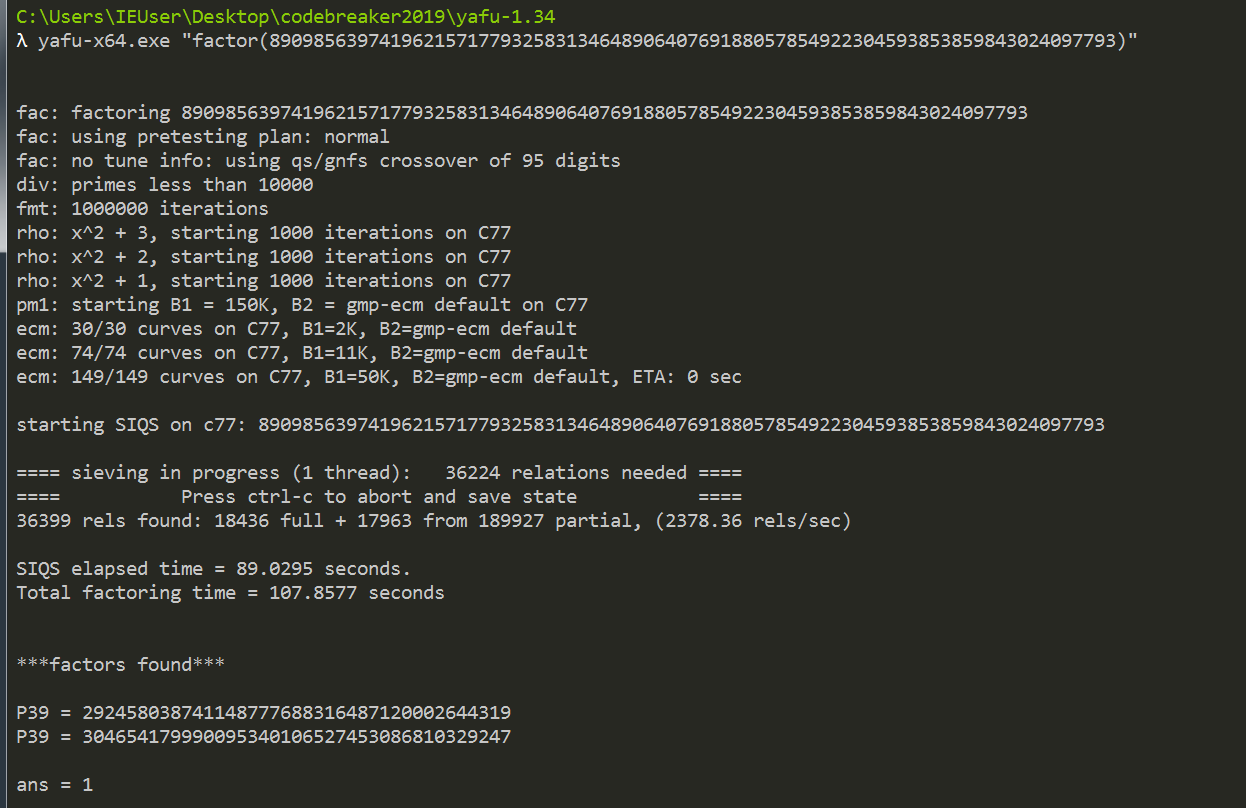
I could recover all the keys if I could get the private key for a 256-bit RSA key. Unlike the other RSA keys, the 256-bit key was exactly 256 bits meaning it was likely not backdoored. There are publicly available tools to factor 256-bit keys. I used yafu, and it was done in a few minutes.
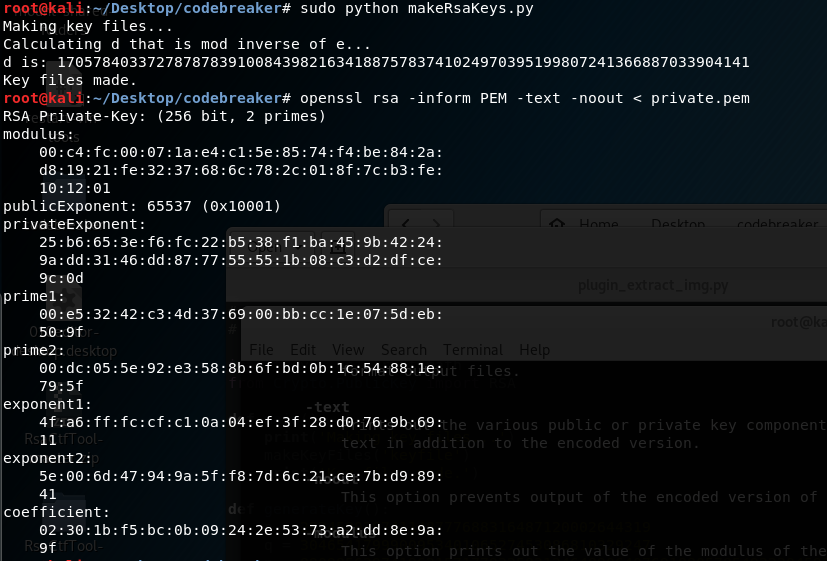
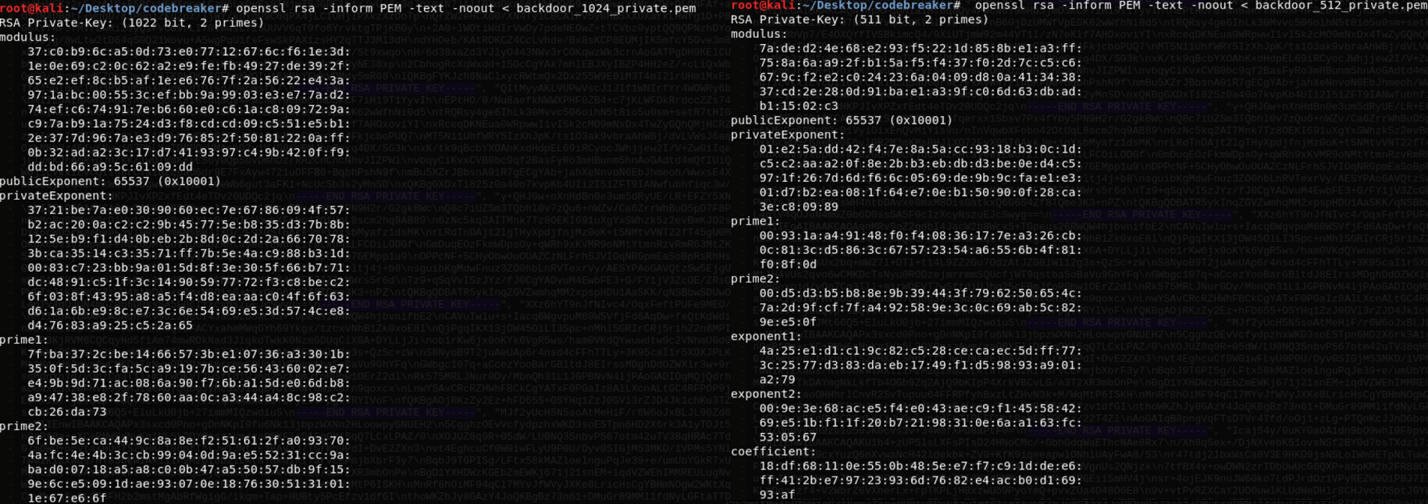
I was then able to recover the private keys for all embedded RSA keys.

Retrieving All Users’ Private Keys
I modified the JavaScript from task 6b to print out a user’s public key, instead of printing and uploading a new key. It requested each TerrorTime user’s public key. I had to log in to a couple users since it will only retrieve a contact’s public key. Next, I recovered the private key for everyone’s public keys, placing each private key into a dictionary with the key’s fingerprint as the dictionary key.

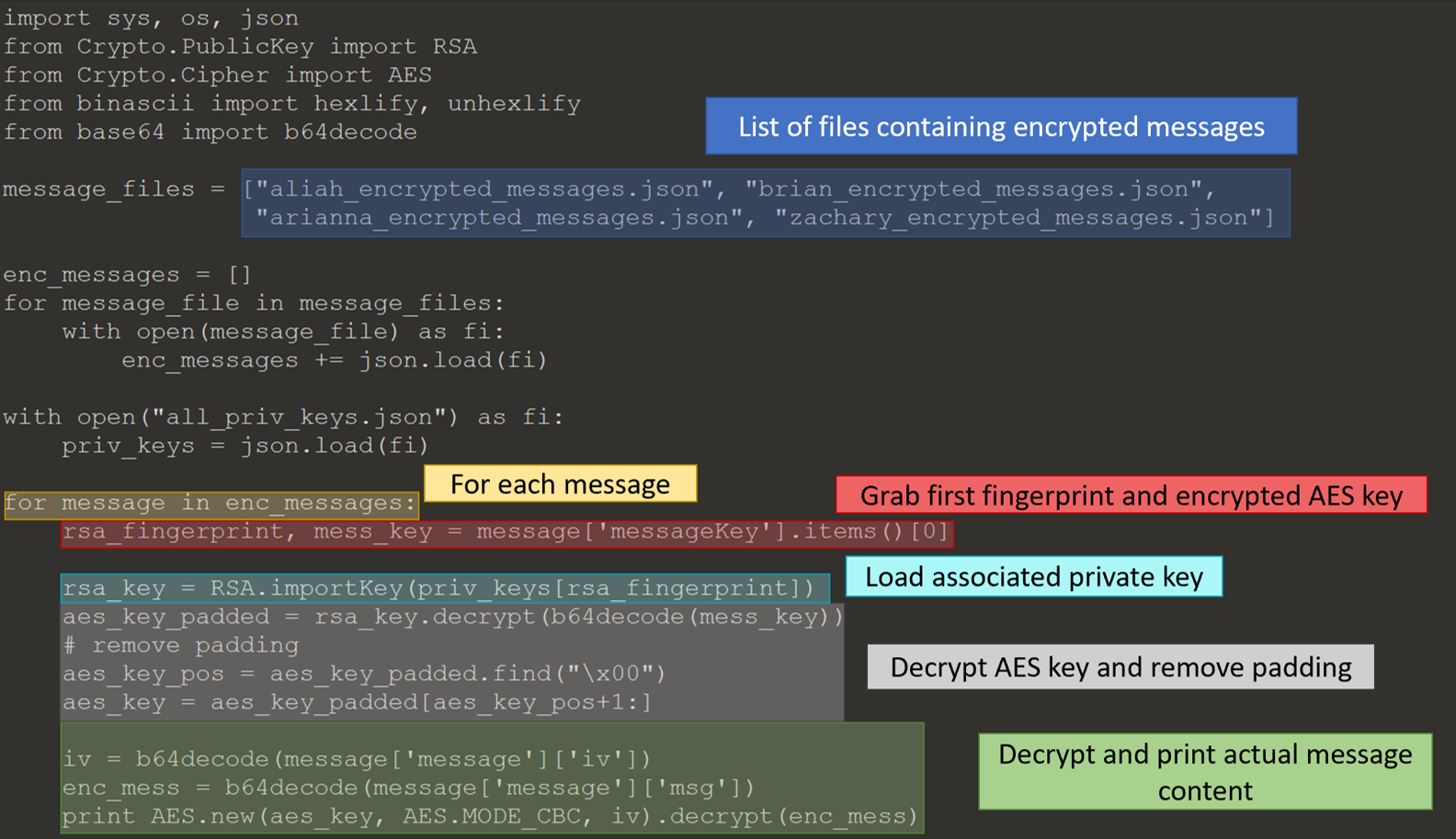
I reused the code from task 5 to pull the messages for each TerrorTime user. Next, I decrypted the messages using the below Python code. It will
- read in the message body,
- retrieve the first finger print and encrypted key,
- look up the corresponding private key using the fingerprint,
- decrypt symmetric key, and
- decrypt the message text.
Determining Actions
I was now able to answer the following questions.
| Question | Answer |
|---|---|
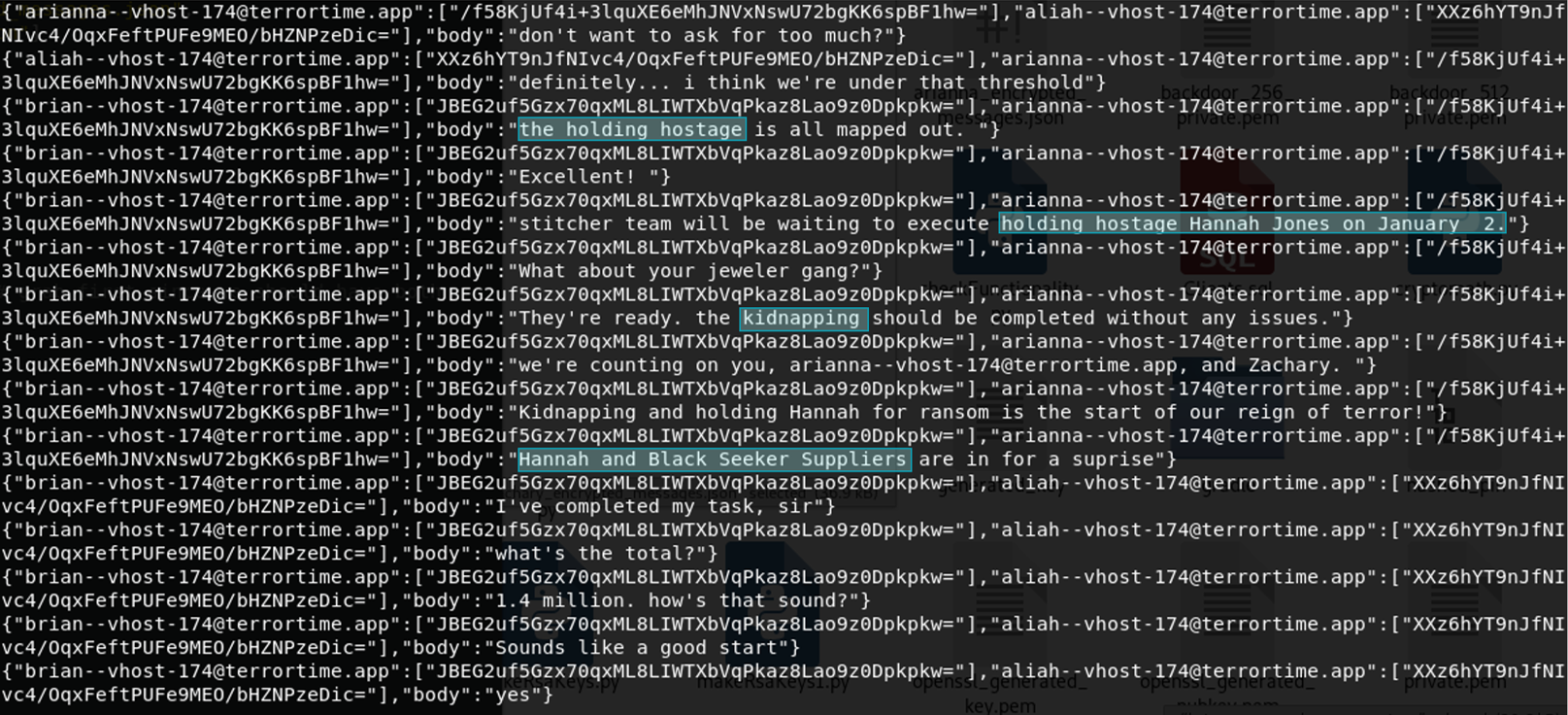
| Plaintext version of the latest encrypted message from the organization leader | definitely... I think we're under that threshold |
| Enter the future action (i.e. beyond the current one) they are planning | assassination |
| The target (of the terrorist action's) identity (First and Last Name) | Hannah Jones |
| The location where the action is to take place | Black Seeker Suppliers |
| Enter the action planned by the terrorists | kidnapping |